前回は行列式について述べましたが覚えていますか？

このような式でしたね。Y＝AXとも表現することができ、Yは出力、Xは入力として考えることができます。Aは入力から出力に変換する係数です。今回もバイアスにあたるBは省略しています。今回はこの式を使って、NN（ニューラルネットワーク）の世界に少し足を踏み入れてみましょう。

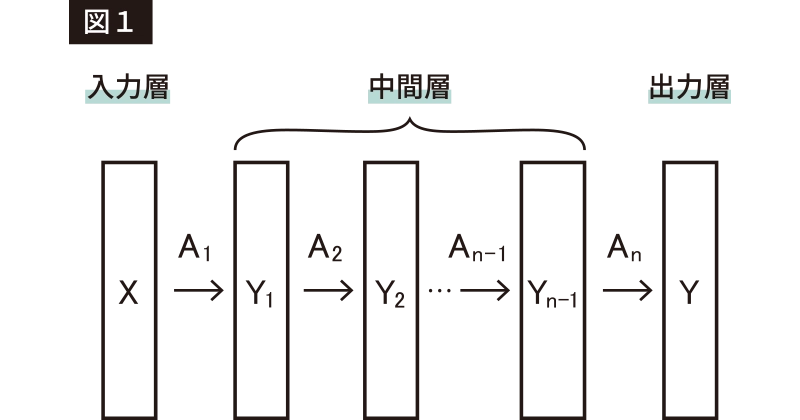
NNは図１のような感じで、入力層、中間層、出力層と大きく分けて3つの層に分かれています。実際には「中間層」は何層もあります。この部分を学習することと、層が何層も重なり深くなっていることから、深層学習と呼ばれたりします。ではこの層をひとつずつ数式で表現してみましょう。入力層（X）から中間層の第１層目（Y1）はY1＝A1X ですね。では中間層の第1層目（Y1）から中間層の第2層目（Y2）はどのように表現できるでしょうか。Y2＝A2Y1 ですね。同じようにして、中間層の第2層目から…と考えていくと、式がどんどん出来上がりますね。Y1から順番に次の層の式に代入して、入力層（X）から出力層（Y）までつなげてみると、

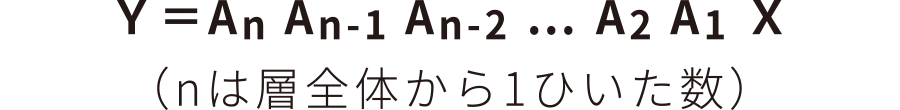
と表現できます。今はAの係数が全部で4つの2行2列の行列ですが、入力や出力の数を変えることで目的に合ったNNを作成したり、Aの係数の行列の数を変えることで（中間層の入力や出力の数を変えることと同じ意味）より複雑なNNを作成したりできます。

しかし、式をよく見ると掛け算がつながっているだけの状態で、例えば1回で×24（24倍）することと、3回で×2×3×4（＝24倍）することが同じになってしまいます。これだと3層の中間層は1層の中間層と変わらないことになります。せっかく3回も層を重ねたのにもったいないですよね。そこでNNでは次の層に伝えるたびに「活性化関数」というものを取り入れて、より複雑なNNを構成しています。「活性化関数」については次回以降に話をします。

今回は皆さんが知っている1次関数を使った表現でNNのイメージを説明しました。いかがでしたでしょうか？