第11回 ニューラルネットワークの式

前回はAIのニューラルネットワークや畳み込みニューラルネットワークで使われている数式について述べました。今回も引き続き数式に触れてみます。
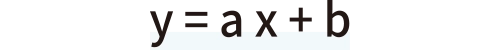
この式、見覚えありませんか?これは中学生の時に学んだことのある1次関数です。aを傾き、bを切片といい、xの値が変わるとyの値も変わっていく式です。ここで2入力1出力のニューラルネットワークを思い出してみましょう。図1のような形です。
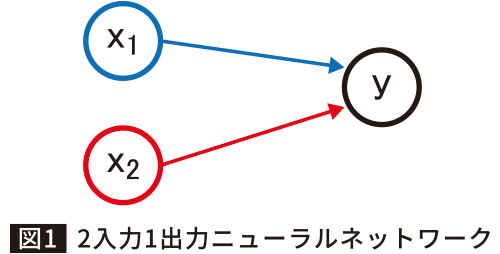
今はbを考えないyを求めてみましょう。yは、

となります。入力が増えるとどのようになるか想像できますか?入力がm個のときyは、
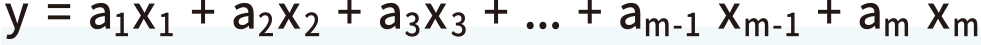
となります。
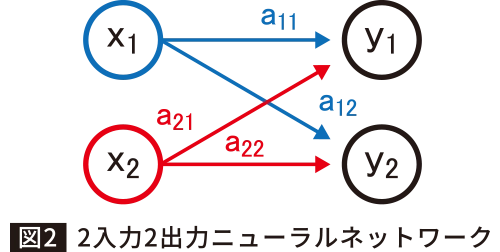
みなさんもご存知のようにニューラルネットワークの出力は複数あります。図2のような2入力2出力のニューラルネットワークを考えてみましょう。aの添え字の前はxの番号、後ろはyの番号にしています。a12だとx1からy2にいく値とわかります。ではこのときのyはどうなっているのでしょうか。yをそれぞれ見てみてみると、
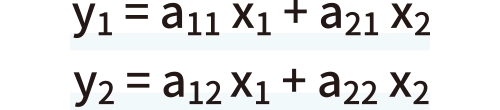
となります。なんだか複雑に見えますね。でも図2を思い浮かべるとイメージしやすいと思います。
これも先ほどと同じように入力がm個になると、

となります。もし入力がm個、出力がn個のニューラルネットワークを考えると…、って考えたくないですね。式がごちゃごちゃしてきたので、yのまとまりをY、aのまとまりをA、xのまとまりをXと考えて、

と書くことができます。また2入力2出力のニューラルネットワークの式をよく見てみると、

こんな式に置き換えることができます。これは行列式といって高校数学では学ぶことが少ない分野ですが、AIではとても重要な位置づけとなっています。
AIではふれたことのない式に出会うことが多いですが、ひとつひとつ順を追ってみると意外と理解できます。最近では理解しやすい書籍が出てきています。本屋で見て面白そうな本を手にとってみてはいかがでしょうか。
「YSeye23号」掲載


